Patrick Frank Publishes on Errors Again

Recently I came across yet another paper by Patrick Frank[1] attempting to claim that climate scientists have been underestimating uncertainties in climate-related data. In this paper, he takes aim at GMST data, and he argues that 

LiG resolution limits, non-linearity, and sensor field calibrations yield GSATA mean ±2σ RMS uncertainties of, 1900–1945, ±1.7 °C; 1946–1980, ±2.1 °C; 1981–2004, ±2.0 °C; and 2005–2010, ±1.6 °C. Finally, the 20th century (1900–1999) GSATA, 0.74 ± 1.94 °C, does not convey any information about rate or magnitude of temperature change.

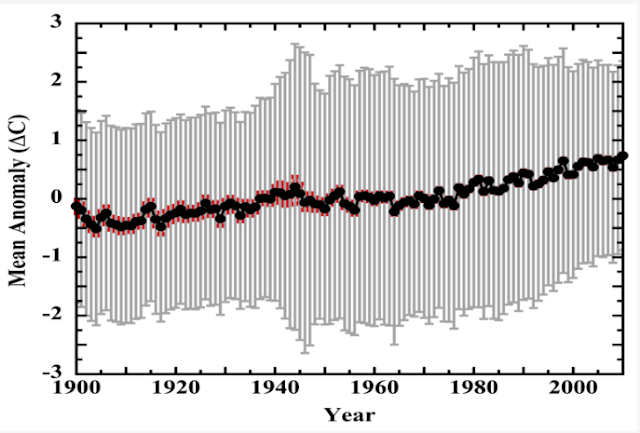
The resulting GMST graph from his calculations is below.

Essentially, he's saying that errors associated with liquid in glass thermometers are so large that we can have no confidence in the global warming trend in the major GMST datasets. Of course, the organizations producing these GMST datasets all evaluate the uncertainties associated with their anomaly values, and their estimates are invariably much smaller - about ±0.05°C in recent decades gradually increasing to ±0.15°C in the late 19th century.[2] These values are also both assessed and published in the peer-reviewed literature. Are all these estimates wrong? Has Patrick Frank discovered something that none of those working with the data have found before? Let's see.

Defining Terms

First let's cover a brief overview of the statistics involved, in very general terms. Frank is attempting to calculate the root-mean-square (RMS) uncertainty at 95% confidence for GMST anomalies. In another post, I talk more about that this means, but essentially what we're after with this calculation is that, given the calculated mean value, we can be 95% confident that the true value falls within the range calculated. So if Frank is right that the during the 20th century the globe warmed 0.74 ± 1.94°C, then we can have very little confidence that the globe has warmed at all, since the range of ± 1.94°C is larger than the calculated mean of 0.74°C. The true value could actually be a negative value to 95% confidence.

Statisticians assess this through calculating a standard deviation (σ). Assuming a normal distribution, 1σ from the mean in both directions will contain 68.2% of the values in the distribution, while a 2σ range includes 95.4% of values the distribution. To calculate the 95% uncertainty, therefore, you can take your 1σ value and multiply it by 1.96; the 95% uncertainty range is slightly less than 2σ. Often this is described generally as the 68-95-99.7 rule, the approximate values for 1σ, 2σ, and 3σ. In many sciences, the 95% uncertainty or ~2σ confidence level is what is required to assess statistical significance.

Some of the issues in this paper come from Fank's attempts to calculate the uncertainty of mean values, given the σ values for the parts of that mean. For instance, to calculate average temperature for a day, scientists simply average the maximum and minimum temperatures for the day.

Tavg = (Tmax + Tmin)/2 or
Tavg = (1/2)*Tmax + (1/2)*Tmin

So the question is, how do you calculate the uncertainty for Tavg given values for σ for Tmax and Tmin? To assess the uncertainty for this average, we can use the following formula

σf^2 = a^2*σ^2a + b^2σ^2b, where

σf = is the 1σ uncertainty of the average
a = fraction of average for thing a
σa = standard deviation for thing a
b = fraction of average for thing b
σb = standard deviation for thing b

Since σf is squared (technically this is variance), we would take the square root of our results of the calculations on the right hand side of the equation to get the 1σ uncertainty. We can then multiply that value by 1.96 to get the 95% uncertainty. If there are more than 2 terms in the average, we can address this as follows:

σf^2 = a^2*σ^2a + b^2σ^2b + ... + n^2σ^2n 

Now what happens if, say you want to calculate the uncertainty of an average, and the uncertainties for each part of the average is the same (σa = σb = ... = σn) and each term contains an equal fraction (a = b = ... = n)? In this case you can simplify the formula substantially to

σf^2 = σ^2/n

Where n is the number of terms. This works because you can distribute out all the σ^2 values, and you're left with all the a^2, b^2, etc values that add up to n/n^2 = 1/n. What we really want to calculate though, is not simply the ~2σ uncertainty. The calculation should be the standard error of the mean (SEM), which is σ/sqrt(N), where N is the number of samples. As we'll see this paper doesn't get that far and ignores 1/sqrt(N) altogether.

The "Misprint" in Frank's Paper

When I'm looking at Frank's paper, equation (6) struck me as odd. Look carefully at how its written.

Frank is calculating the ~2σf (technically 1.96*σf) uncertainty for the land-surface air temperature mean by propagating uncertainty from monthly uncertainties, but look carefully at what's in the radical. What should be clear is that it could be easily rewritten as (12/12)*(0.198)^2. The 12/12 cancels out, and you're left with =sqrt(0.198^2), which also reduces simply to 0.198. In other words, all Frank is doing is taking the monthly σ=0.198 and calculating the 95% uncertainty of the monthly σ value. And the answer isn't correct, because 1.96*0.198 = 0.388°C. Something is wrong here, and the reason is he got the formula wrong. This is what he should have calculated:

~2σf  = 1.96*sqrt((0.198^2)/12) = ±0.112°C

It turns out that others have noticed this too on Skeptical Science, and there's much more to be said about this. From the Skeptical Science summary, I think we can detect where Frank's error began. It begins in equation (4), where Frank incorrectly wrote the formula (making the same mistake he made in equation 6) but he got the right answer.

The solution to this equation is ±0.541°C, so why did he say it's ±0.382°C? Notice he's calculating the ~2σ uncertainty for Tavg based on the uncertainties for the Tmax and Tmin values, but he didn't square the a and b terms, both of which are 1/2 (since day and night average half the day). The variance equation should be σ^2  = (1/2)^2*(0.366^2) + (1/2)^2*(0.135^2) , which simplifies to (0.366^2 + 0.135^2)/4, and if you take the SQRT of that and multiply by 1.96, you get ±0.382°C. Frank published a comment to his paper pointing out that the 2 should have been outside the radical, and calls it a misprint. Sure enough, if he took the 2 outside the radical, he'd get the right answer, but technically, given the logic of what he's calculating, it would be better to write it as a 4 inside the radical.

And it's this misprint (error?) that explains Frank's mistake in equation 6. The 12 in the denominator should have been 12^2. That is, inside the radical the equation should be (12/12^2)*(0.198^2), which simplifies to (0.198^2)/12. In equation 4, he printed the misprint but calculated the correct result because he didn't calculate the result from the equation he wrote. In equation 6, he calculated the incorrect result from the "misprint" in the equation. And he did the same thing in equation 5.

This equation reduces simply to 1.96*0.195. All he did is calculate the ~2σ uncertainty for the daily 1σ value. The correct value would be 

~2σf = 1.96*sqrt((0.195^2)/30.417) = ±0.069°C

And again, he made the same mistake when calculating the uncertainty for combining global land with SSTs in equation (7).

The 0.7 and 0.3 terms should both be squared in this equation. The correct calculation would be

~2σf =1.96*sqrt((0.7^2)*(0.136^2)+(0.3^2)*(0.195^2)) = ±0.219°C

All of these equations were written incorrectly, and in all but equation (4), these "misprints" caused him to make incorrect calculations that inflate uncertainties by a significant margin. 

SEM and 1/sqrt(N)

And this is not the end of the errors and oversights in this paper. There is more going on here that's wrong. For instance, increasing the number of values (N) should decrease uncertainty. The more values you average, the less the uncertainty in the mean. Frank does not calculate SEM with a 1/sqrt(N) term. Frank's reasoning for not including this appears to be

Correlated and non-normal systematic errors violate the assumptions of the central limit theorem, and disallow the statistical reduction of systematic measurement error as 1/√𝑁.

But this is simply false. As has been clearly demonstrated many times, averaging multiple values increases the precision of the average. This is something you can test for yourself. Take 100 values accurate to 2 decimal places. Then duplicate those values except round them to 1 decimal place. Then average both sets of 100 values. You'll find the both averages are similar to each other, and if you do the same with 1000 values, they will be even closer . This is because while rounding introduces error, the error is random - about half add to the mean and about half subtract from the mean, so the more values you average, the closer the two columns will agree. Since averaging cancels out much of the random error, the loss of precision where N=100 scales by σ/sqrt(100).

Systematic errors are also accounted for and quantified, and bias correction reduces their impact in all modern GMST datasets. Biases also work in both directions and can cancel each other out. If one bias adds 0.1°C to a value and two other biases subtract 0.05°C, their net effect is essentially 0. Bias correction makes the net effect of all biases small. There are numerous papers quantifying biases and correcting them to remove their impact on temperature trends. There is no justification for removing the 1/sqrt(N) term from the SEM. Uncertainties of GMST anomalies are dominated by sampling issues, not by instrumental error. Because Frank neglected to calculate SEM, his uncertainty estimates are going to be way too high even after making the above corrections to his equations. 

And Skeptical Science observes that Frank has also not properly accounted for covariance in these calculations, which would introduce a 2ab*σab term into his equation. The Skeptical Science article observes that one reason why scientists use anomalies is to reduce this uncertainty.

But anomalies involve subtracting one number from another, not adding the two together. Remember: when subtracting, you subtract the covariance term. It’s σf^2 = a^2*σ^2a + b^2*σ^2b - 2ab*σab. If it increases uncertainty when adding, then the same covariance will decrease uncertainty when subtracting. That is one of the reasons that anomalies are used to begin with!

Conclusion

I don't see the need to detail these errors more completely. I think the case can be sufficiently made from the above that Frank has not done his due diligence in this paper to provide a competent analysis of GMST uncertainties. The uncertainties calculated in the peer-reviewed literature for the major GMST datasets are competently done, and they do not make these kinds of mistakes. There's no reason to discard the competent analysis in the peer-reviewed literature for the error-prone analysis in Frank's paper.

References:

[1] Frank P. LiG Metrology, Correlated Error, and the Integrity of the Global Surface Air-Temperature Record. Sensors. 2023; 23(13):5976. https://doi.org/10.3390/s23135976

[2] Lenssen, N. J. L., Schmidt, G. A., Hansen, J. E., Menne, M. J., Persin, A., Ruedy, R., & Zyss, D. (2019). ImpImprovements in the GISTEMP uncertainty model. Journal of Geophysical Research: Atmospheres, 124, 6307–6326. https://doi.org/10.1029/2018JD029522