Bias Correction in Surface Thermometer Datasets

Virtually all temperature datasets that have been around for a significant amount of time depend on surface thermometers, most of which were not designed to measure climate changes; they were positioned to collect meteorological data for temperature and precipitation, and many of these stations have been maintained by volunteers. In earlier years there was no standardized process for even when temperatures were recorded. Daily temperatures were calculated using max-min thermometers that recorded the "max" and "min" temperatures recorded by the thermometer since the last time it was checked and reset. If the thermometer was checked daily, this would give data for daily highs and lows. The average temperature for the data as calculated simply by Tavg = (Tmax + Tmin)/2. Biases can easily enter into the temperature record by systematic changes in 1) time of observation, 2) instrument technology, and 3) urbanization, as well as other factors. Likewise, sea surface temperatures were largely taken from ships, where data collection methods could significantly altar the temperatures collected - systematic changes in collection methodology introduces significant bias into the temperature record.

The data collected from these networks of surface thermometers are indisputably affected by non-climactic biases that can alter calculated trends away from the true climate trend. Bias correction is designed to quantify these biases and correct for them. In this post, I'm not going to identify all sources of bias; that would make this post way too long, and I think it would be more interesting to cover these in separate posts, but I'll include in my list of references some of the most significant papers in the peer-reviewed literature that identify sources of bias, quantify them and correct them. Many of these corrections can be performed automatically by what is called "homogenization" - that is, it identifies individual stations that produce spurious results with respect to their neighbors and correct for these spurious readings.

However, I frequently read people saying that homogenization is orchestrated by scientists to generate a spurious warming trend that wouldn't otherwise exist, or perhaps to exaggerate warming trends so that climate data can be engineered to support the alarmism of climate scientists. What I want to do here is show what the overall effect of bias correction is, so we can evaluate these claims. When we do, we can easily see that these claims are objectively false. We'll see this first in global temperature data and then in US temperature data.

Global Data

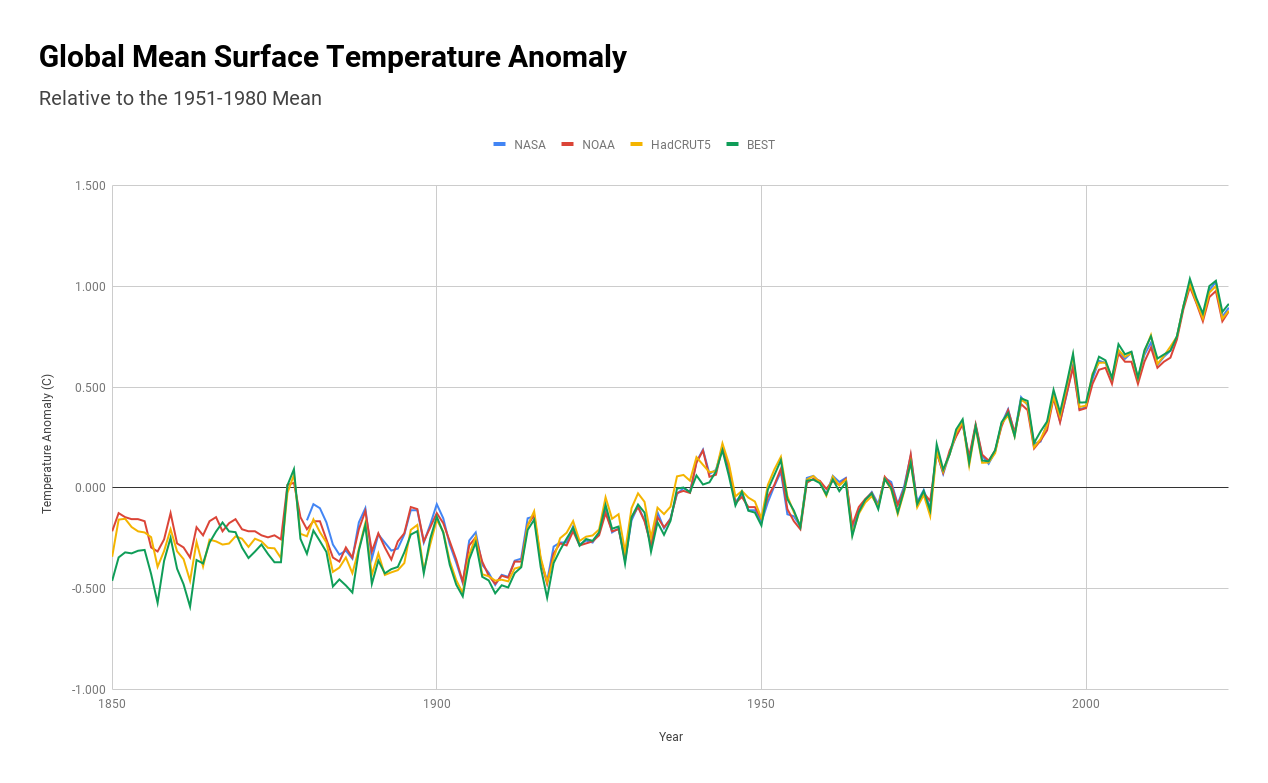
All major datasets for global mean surface temperature use bias correction. I'll refer to these major GMST datasets as "homogenized" datasets. Bias correction does not altar the original station data. The corrections are applied within the homogenized datasets, leaving the raw station data unaltered. This means we can compare homogenized data to raw data to quantify the effect of bias correction on global temperatures. To do this properly, we need to generate an "uncorrected" dataset calculating GMST from raw station data without the application bias corrections. Performing this type of analysis on global land data, global sea surface temperature data, and global land + ocean data reveals some things very clearly:

1. Bias correction lowers past temperatures on land, so homogenized land temperatures show more land warming than uncorrected land temperature.
2. Bias correction increases past temperatures prior to 1940 for sea surface temperatures, so homogenized SSTs show less warming than uncorrected SSTs.
3. SST corrections are larger than land corrections (and the oceans take up more surface area than land) so the net effect of bias correction is that homogenized global data shows less warming than uncorrected global data.

CarbonBrief did an analysis of bias correction and showed the effects of bias correction on land and SST data. I'm including all three graphs generated by CarbonBrief below:

Adjustments to Land Temperatures Increase Warming Trends

Adjustments to SSTs Decrease Warming Trends

Adjustments to Global (Land + Ocean) Temperatures Decrease Warming Trends

Recently NOAA updated their GMST dataset from v5 to v5.1 to include more geographic coverage, and they also extended the dataset back to 1850. I found their uncorrected data for 1880-2016, so I plotted all three so to verify that what CarbonBrief published is essentially correct. Overall, bias correction decreases global warming trends by increasing temperatures before 1940, since bias corrections are dominated by corrections to SSTs. This is due to systematic changes in collection methodologies around 1940.

Adjustments to Global (Land + Ocean) Temperatures Decrease Warming Trends

What this means necessarily is that scientists are not manufacturing global warming using homogenization to introduce spurious warming trends in to temperature data. If anything, scientists are doing the opposite. Removing non-climactic biases essentially removes spurious warming from the global temperature record revealing that the true climate trend is slightly less than what the uncorrected dataset would indicate.

US Temperatures

But what about US temperatures? We've seen above that bias correction for land temperatures cools the past and slightly increases the land warming trend. Could it be that scientists are using bias correction to generate spurious warming trends in the US to make US temperatures fit "alarmist" predictions of warming and extreme heat in the US? Well, it turns out we can test that too.

Until recently, NOAA's US temperature dataset was USHCN, and over time, updates to this dataset introduced bias correction techniques to remove non-climactic biases from the dataset. Recently, NOAA deprecated USHCN in favor of nClimDiv, and in 2005, they introduced a more sophisticated network of stations that are ideally sited and specifically designed to collect climate data for the US, called USCRN. The USCRN network contains far fewer stations - it currently has 114 CONUS stations, 21 stations in Alaska and 2 in Hawaii. The USCRN network has been operating since 2005 and requires no bias correction. It is essentially a "raw" dataset that can be compared to the much larger but homogenized nClimDiv. 

Comparison of Raw USCRN with Homogenized nClimDiv

So I downloaded both datasets from 2005 to present and compared the two for the time periods for which they overlap. A couple observations are immediately obvious:

1. The two datasets are statistically identical - that is, the differences between the CONUS averages in the two datasets are not large enough to show any statistically significant difference in trends.
2. The calculated best fit line between the two show that nClimDiv has slightly less warming than USCRN. Using Google Sheets, I calculated the 2005 to present trends for USCRN to be 0.337 ± 0.298°C/decade and for nClimDiv to be 0.256 ± 0.299°C/decade (2σ). They are not statistically different from each other, but the calculated best fit line in the uncorrected dataset shows a slightly steeper slope than the homogenized dataset.
3. Since the USCRN dataset has only 18 years of data, there is little we can say here regarding climate trends (the nClimDiv trend isn't even statistically significant yet), but what this shows is that homogenization is not causing spurious warming not seen in pristine, raw data.

Above is a graph from a Climate Brink article from Zeke Hausfather making the same point. The calculated trend in USCRN is warming perhaps 30% faster than ClimDiv, which actually agrees with  the warming rates measured in NOAA's global dataset. So if anything, homogenized data underestimates warming rates in the US with respect to USCRN data.

Update (2/1/204). So you can see more clearly how USCRN and nClimDiv compare, here I plotted the  linear trendlines for both datasets and then nClimDiv-USCRN. The downward slope of the difference time series means that USCRN is warming slightly faster than nClimDiv, and it cannot be that there's a spurious warming trend in nClimDiv with respect to USCRN. I expect as more years are added to USCRN, the slope of the difference line will get smaller, but this is where it is now.

Conclusion

This analysis should put to rest any notion that scientists are using bias correction to fabricate or exaggerate warming trends. It's simply not happening. Global uncorrected data shows more warming than global homogenized data, and USCRN is statistically identical to nClimDiv (with calculated trends showing slightly more warming in the uncorrected dataset).

In other posts, I cover some other issues related to this. Rather than repeating myself here, I'll refer you to these other posts:

1. Satellite datasets have far greater structural uncertainties than surface thermometers, and the bias correction applied to satellite datasets far exceeds those applied to surface thermometers.
2. Older versions of "global" datasets from the 1980s often are land only and lack the geographic coverage than updated versions, since data from station networks have been added to global datasets with time.
3. Urbanization does introduce bias into temperature trends, but homogenization effectively removes that bias such that the most rural stations are warming at about the same rate as all stations. So we cannot attribute any of the increase in global temperatures to urbanization.
4. Much of the misinformation I'm addressing here is promoted by Tony Heller, and I've collected an extensive set of resources addressing his false claims, many of which have to do with his failure to understand how bias correction works. 

In future posts, I plan to cover other related issues, such as bias correction for time of observation, the application of bias correction to SSTs, and the importance of using a grid or some other form of area-weighted averaging to avoid introducing bias into datasets.

Resources on Bias Correction and Related Issues:

[1] Jones P. D., T. J. Osborn, and K. R. Briffa. “Estimating sampling errors in large-scale temperature averages.” Journal of Climate 10.10 (1997): 2548–2568. https://doi.org/10.1175/1520-0442(1997)010%3C2548:ESEILS%3E2.0.CO;2

[2] Folland C. K., et al. “Global temperature change and its uncertainties since 1861.” Geophysical Research Letters 28.13 (2001): 2621–2624.
https://doi.org/10.1029/2001GL012877

[3] Brohan P et al. “Uncertainty estimates in regional and global observed temperature changes: A new data set from 1850.” Journal of Geophysical Research: Atmospheres 111.D12 ( 2006) https://doi.org/10.1029/2005JD006548

[4] Menne, M.J. and C. N. Williams Jr. “Homogenization of Temperature Series via Pairwise Comparisons.” Journal of Climate 22 (2009): 1700-1717. http://dx.doi.org/10.1175/2008JCLI2263.1

[5] Morice, C. P., et al. “Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: The HadCRUT4 data set.” Journal of Geophysical Research: Atmospheres 117.D8 (2012): D08101.
https://doi.org/10.1029/2011JD017187

[6] Rohde, R. “Berkeley earth temperature averaging process.” Geoinformatics & Geostatistics: An Overview 1.2 (2013):1000103.
https://www.scitechnol.com/berkeley-earth-temperature-averaging-process-IpUG.php?article_id=582

[7] Smith, Thomas M. and Richard W. Reynolds, “Bias Corrections for Historical Sea Surface Temperatures Based on Marine Air Temperatures,” Journal of Climate 15 (2002): 73-87.
https://www.ncdc.noaa.gov/monitoring-references/docs/Smith_Reynolds_2002.pdf

[8] Karl et al, “A Model to Estimate the Time of Observation Bias Associated with Monthly Mean Maximum, Minimum and Mean Temperatures for the United States,” Journal of Applied Meteorology 25.2(1986):145-160
https://doi.org/10.1175/1520-0450(1986)025<0145:AMTETT>2.0.CO;2
https://www1.ncdc.noaa.gov/pub/data/ushcn/papers/karl-etal1986.pdf

[9] Vose et al, “An evaluation of the time of observation bias adjustment in the U.S. Historical Climatology Network,” Gheophysical Research Letters 30.20 (2003).
https://www1.ncdc.noaa.gov/pub/data/ushcn/papers/vose-etal2003.pdf?fbclid=IwAR21nb0Nu1Wbr_oUwj2VRUjOkEM9GRyjd7xyXETP2SgT9cybcMUDNiRG7Pw

[10] Peterson and Owen, “Urban Heat Island Assessment: Metadata Are Important” Journal of Climate 18 (2005): 2637-2646.
https://journals.ametsoc.org/doi/10.1175/JCLI3431.1

[11] Venema, V. et al 2012. Benchmarking homogenization algorithms for monthly data. Clim. Of the Past, 8, 89-115.

[12] Mestre, O. et al 2013. HOMER: HOMogenisation software in R – methods and applications. Idöjárás, 117, 47-67.

[13] Szentimrey, T. 2008. Development of MASH homogenization procedure for daily data. Proceedings, 5th seminar for homogenization and quality control in climatological databases, Budapest, Hungary, 2006, WCDMP- No.71, 123-130.

[14] Wang, X.L., Chen, H., Wu, Y., Feng, Y. and Pu, Q. 2010. New techniques for detection and adjustment of shifts in daily precipitation data series. J. Appl. Meteor. Climatol., 49, 2416-2436.

[15] Willett, K. et al 2014. A framework for benchmarking of homogenisation algorithm performance on the global scale. Geosci. Instrum, Method. Data Syst., 3, 187-200.

[16] NOAA, “Monitoring Global and U.S. Temperatures at NOAA's National Centers for Environmental Information”
https://www.ncdc.noaa.gov/monitoring-references/faq/temperature-monitoring.php

[17] Quayle, R. G., Easterline, D. R., Karl, T. R., & Hughes, P. Y. (1991). Effects of Recent Thermometer Changes in the Cooperative Station Network, Bulletin of the American Meteorological Society, 72(11), 1718-1724. https://journals.ametsoc.org/view/journals/bams/72/11/1520-0477_1991_072_1718_eortci_2_0_co_2.xml