The Physics of the Climate Response to Doubling CO2

Update (6/6/2025): I edited the text for clarity (especially in the first couple paragraphs), changed g to g̃ to distinguish the normalized GHE from the acceleration due to gravity, and added more references with excerpts at the bottom of the post.

The Earth's effective temperature - the mean surface temperature of Earth if the atmosphere contained no GHGs but with current albedo can be calculated since we know that ASR (hereafter Fin) = (1-α)*S/4 and OLR (hereafter Fout) is governed by εσ*T^4. At equilibrium, ASR = OLR (Fin = Fout). With no greenhouse effect (GHE), the Earth's emission temperature (Te) would be at the surface, meaning that Te = Ts, so we can solve for Te with

(1-α)*S/4 = εσ*Te^4

If we solve for Te with a surface emissivity (ε) of 0.98 and albedo (α) of 0.306, we end up with Te = 255.3 K. So, if the earth had no atmosphere with albedo roughly the same as today, the average surface temperature of the earth would be about -18°C. However, we know that currently, the earth is about 33°C warmer than this; it's ~288 K or 15°C. The ~33°C difference is caused by the GHE. Greenhouse gases prevent thermal radiation from escaping into space, trapping heat in the troposphere, such that the surface can't cool to its effective temperature. As GHGs increase in concentration, GMST warms in response.

I decided it would be fun to explain how this works given the physics accounting for various fluxes that influence the Earth's surface temperature. What I want to do is describe current climate physics at explains the current conditions at 33K above 255K and then consider the impact of doubling CO2 with an ECS of 3°C. This will show how perturbations of the carbon cycle cause change in temperature, though even with positive feedbacks amplifying CO2 forcings, we don't get runaway warming like what we see on Venus. This is a very simplified model considering only the effect of 2xCO2  + feedbacks.

Current Conditions

                                Climate at Equilibrium to 288 K

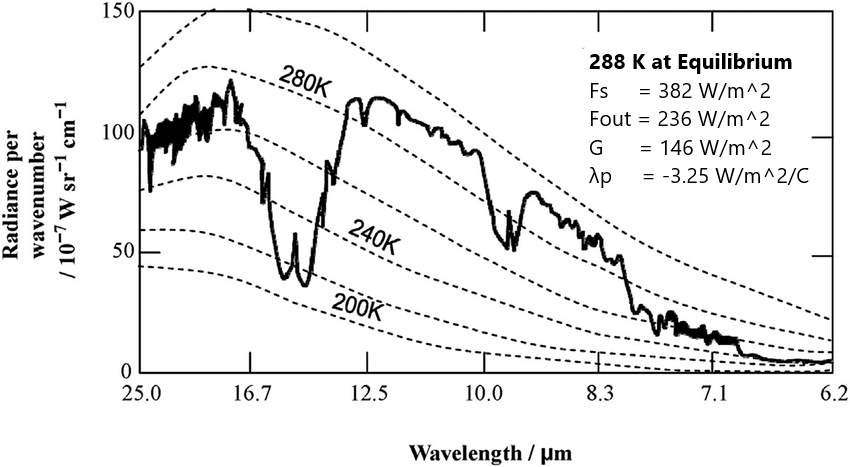
To explain current conditions, we need to start with current surface temperature (Ts) at 288 K and then calculate the upwelling flux of long wave (LW) radiation from the surface (Fs) as

Fs = εσT^4 = εσ*288^4 = 382.3 W/m^2 (1)

The outgoing longwave radiation flux near the top of the atmosphere flux (OLR or Fout) and incoming absorbed solar radiation (ASR or Fin) are nearly identical - the difference between the two is the earth's energy imbalance, currently about 1 W/m^2. The value of incoming solar flux can be calculated (where α is albedo and S = TSI) as

Fin = (1-α)*S/4 = (1-0.306)*1361/4 = 236.1 W/m^2 (2)

At equilibrium, Fin and Fout would therefore equal each other at 236 W/m^2, so the difference between the values from (1) and (2) is the greenhouse effect (G). This effect is the amount of thermal radiation emitted from the surface doesn't escape into space. That is, if the atmosphere were free of greenhouse gases, then Ts = Te and Fs = Fin = Fout. So

G = Fs - Fout = 382.3 - 236.1 = 146.2 W/m^2 (3)

The ratio G/Fs is the normalized greenhouse effect (g̃) - essentially it's the fraction of Fs emitted from the surface that doesn't escape to space. While technically this value increases with temperature, for small increases in Fs, it can be treated as a constant, g̃ remains roughly the same. So

g̃ = (Fs - Fout)/Fs = G/εσT^4 = 146.2/382.3 = 0.38 (4)

Consistent with the IPCC[2], I'm holding g at ~0.4. Solving this for Fout, we can actually determine Fout if we know both g̃ and Fs

Fout = (1−g̃)*Fs = (1−g̃)*εσT^4 (5)

If we differentiate the above Stephan-Boltzmann equation, we can estimate the Planck Response, which allows us to account for the fact that warmer objects radiate more than colder objects. That is to say, as the planet's surface warms, there's an increase increase in planetary infrared energy loss; it is this increase in surface radiation that increases Fout until it matches Fin again. The Planck Response is is a negative feedback (so I'm using (g̃-1) instead of (1-g̃) to give the result a negative sign) and per the IPCC,[2] this can be calculated as:

λp = δF/δT = (g̃-1)*4εσT^3 = -0.6*4*0.98*σ288^3 = -3.28 W/m^2/C (6)

The values from these 6 equations are non-controversial, though their precise values can be better estimated by other means than the simple model I'm using.[5][6] What I want to do here is simply show how the math works so that when there's a perturbation of the Earth's energy imbalance from a doubling of CO2, the earth warms until it reaches a new equilibrium at a higher temperature. I want to show how this works using a standard estimate for ECS = 3°C and feedbacks (λt) from water vapor, clouds, etc. without leading us into a runaway greenhouse effect like what we see on Venus.  

Doubling CO2 Before Feedbacks

If we double CO2, the emission temperature (Te) moves to a higher altitude, and more energy is "trapped" in the climate system. The surface temperature (Ts) warms in response, since it can no longer cool as effectively as it could when CO2 was lower. As Ts increases, surface radiation also increases until Fout = Fin = 236 W/m^2.

                          Climate at Equilibrium to 291 K (2xCO2 with ECS = 3°C) 

Above I showed the incoming flux of solar radiation (Fin) to be 236 W/m^2, and if the Earth was at equilibrium with no greenhouse effect, the flux escaping the earth would be identical to that value. Using the Earth's effective temperature (255 K), and the Stefan-Boltzmann equation, we can calculate

Fout = εσT^4 = εσ*255.3^4 = 236 W/m^2

This is roughly equivalent to the Fin calculation above, confirming that without the influence of greenhouse gases, the Earth's temperature would be stable at about 255 K.

A perturbation of the Earth's Energy Imbalance (EEI), in this case, from doubling CO2 (ΔFco2), causes 5.35*ln(2) = 3.71 W/m^2 increase in radiative forcing - more energy enters the climate system than escapes into space. This means that while Fin remains the same, Fout decreases by 3.7 W/m^2. The surface of the planet must warm until the imbalance is restored to 0 and Fout = Fin. To calculate the sensitivity before feedbacks (what we can call the Planck Sensitivity), we can divide the forcing for doubling CO2 by the Planck Response.[4] This yields 

ΔFco2/λp = 3.7/3.28 = 1.13°C 

This is essentially the same calculation as combining the Stefan-Boltzmann equation with its derivative[4]. If we do that with the Earth's current temperature (288 K) we essentially the same result:

ΔT/T = (1/4)*ΔFco2/Fin, so

ΔT = T(ΔFco2/4Fin) = 288*(3.7/4*236.1) = 1.13°C

A Planck Sensitivity of 1.13°C is also consistent with what is produced in model calculations.

Doubling CO2 After Feedbacks

As the surface of a planet warms, it radiates more toward space than when it was cooler. This is again expressed in what is called the Planck Response or Planck Feedback (λp), which, as you can see from equation (6), increases with temperature. As greenhouse gases increase in the atmosphere, these GHG forcings are amplified by positive feedbacks and dampened by negative feedbacks. These feedbacks can affect either or both of Fin and Fout, but for the sake of illustration here, we'll hold Fin to a constant 236 W/m^2. Either way, though, the total of these feedbacks (λt) is always smaller than -λp. Since the Planck Feedback increases with temperature, perturbations of EEI can always be restored to a new equilibrium temperature.

The energy imbalance caused by doubling CO2 requires that a new, higher equilibrium temperature be achieved by increasing the upwelling surface LW flux (Fs) - that is, the surface temperature must increase. With ECS = 3°C, doubling CO2 increases surface temperature from 288 K to 291 K. The resulting Fs would thus become

Fs = εσT^4 = εσ*291^4 = 398.5 W/m^2

This increases the greenhouse effect (G) to  398.5 - 236.1 = 162.4 W/m^2, assuming constant ASR. That's an increase of 162.4 - 146.2 = 16.2 W/m^2 to the greenhouse effect. Because the Earth's surface is now at a higher temperature, the Planck Response must also increase. The Planck Feedback (λp) at 291 K is

λp = (g̃-1)*4σT^3 = -0.6*σ291^3 = -3.35 W/m^2/C. 

We can multiply this value by ECS = 3°C to get a total of -3.35*3 = -10 W/m^2 for the Planck response for this perturbation of the Earth's energy imbalance. This means that the total of all feedbacks λt need to account for the difference between ΔFco2 and -λp*ECS or 6.3 W/m^2. This implies that total feedbacks (λt) 6.3/3 = 2.1 W/m^2/C.[3]

λp*ECS + ΔFco2 + λt*ECS = 0

-10 W/m^2 + 3.7 W/m^2 + 6.3 W/m^2 = 0 W/m^2 

We would write this another way. An ECS of 3°C expressed as a response to 2xCO2 would be 3.71/3 = 1.237 W/m^2/C (λc), so we can rewrite the above as

-λp = λc + λt 

3.35 W/m^2/C = 1.24 W/m^2/C + 2.1 W/m^2/C

In other words, forcings + feedbacks = -Planck Response. Even though my example is admittedly oversimplified by having all feedbacks affect Fout instead of Fin, the results would not change with feedbacks that affect Fin or ASR. That is, feedbacks that decrease albedo (like decreases in low cloud cover) still create a gap between Fin and Fout that is closed by warming. It's the imbalance (Fin - Fout) that determines how much surface warming occurs, whether that difference is caused by changes in Fin, Fout or both.

Conclusion

This means that a new equilibrium will have been reached at 291 K when EEI is reduced to 0. This new equilibrium is reached at 291 K if ECS = 3°C, λp = -3.35 W/m^2/C at the resulting 291 K, and λt = 2.1 W/m^2/C. However, there are other combinations of values that would also add to 0 at a different equilibrium temperature. Increasing ECS would also increase -λp and λt. Likewise, decreasing ECS would decrease -λp and λt.  For various ECS values in the IPCC's range, here are the results you would get:

        For ECS = 2.5°C        λp = -3.34 W/m^2/C        λt = 1.85 W/m^2/C

        For ECS = 3.0°C        λp = -3.35 W/m^2/C        λt = 2.12 W/m^2/C

        For ECS = 3.5°C        λp = -3.37 W/m^2/C        λt = 2.31 W/m^2/C

        For ECS = 4.0°C        λp = -3.39 W/m^2/C        λt = 2.46 W/m^2/C

So this isn't proof that ECS = 3°C. However, warming rates are consistent with an ECS near 3°C.  These calculations do show that runaway warming like Venus is not really something to be concerned about, since this would require that at some point λt > λp and from that point λt increases with temperature at least as rapidly as λp increases. But this is not at all likely. Perhaps more significantly, it also shows that to the extent we can constrain estimates for λt, we can also limit reasonable values for ECS. Likewise, constraining our estimate of ECS would also limit reasonable values for λt. The values for ECS, λt and λp cannot just be anything. They are related to each other and bound by known laws of physics. Constraining these values will continue to improve model simulations and predictions, but the the constraints that the laws of physics place on these values make it possible to understand the climate-related response to these perturbations to make reliable assessments of how the Earth's climate system will respond to doubling CO2.

References:

[1] Gavin Schmidt, "The CO2 problem in 6 easy steps." RealClimate. Aug 6, 2007.
https://www.realclimate.org/index.php/archives/2007/08/the-co2-problem-in-6-easy-steps/

[2] IPCC AR6 WG1. https://www.ipcc.ch/report/ar6/wg1/. For the Planck Response, see: https://www.ipcc.ch/report/ar6/wg1/chapter/chapter-7/#7.4.2.1: "The multi-kernel and multi-model mean of α P is equal to –3.20 W m–2°C–1for the CMIP5 and –3.22 W m–2°C–1for the CMIP6 models (Supplementary Material, Table 7.SM.5). Overall, there is high confidence in the estimate of the Planck response, which is assessed to be α P= –3.22 W m–2°C–1 with a very likely range of –3.4 to –3.0 W m–2°C–1 and a likely range of –3.3 to –3.1 W m–2°C–1."

[3] Sherwood, S. C., Webb, M. J., Annan, J. D., Armour, K. C., Forster, P. M., Hargreaves, J. C., et al. (2020). An assessment of Earth's climate sensitivity using multiple lines of evidence. Reviews of Geophysics, 58, e2019RG000678. https://doi.org/10.1029/2019RG000678

[4] The IPCC refers to Planck Sensitivity as the "The Planck temperature response" or "ΔTP" which is defined as "the equilibrium temperature change in response to a forcing ΔF when the net feedback parameter is equal to the Planck response parameter: ΔTP = –ΔF/αP." The second, essentially equivalent formula (ΔT = T*ΔFco2/4Fin), can be derived from F = εσT^4 and its derivative, δF/δT = 4εσT^3. Reorganizing terms we get εσ=F/T^4 and εσ=δF/δT*4T^3, and combining equations gives us δF/4F = δT/T.

[5] Cronin, T. W., & Dutta, I. (2023). How well do we understand the Planck feedback? Journal of Advances in Modeling Earth Systems, 15, e2023MS003729. https://doi.org/10.1029/2023MS003729

[6] Bony, S., Colman, R., Kattsov, V. M., Allan, R. P., Bretherton, C. S., Dufresne, J.-L., et al. (2006). How well do we understand and evaluate climate change feedback processes? Journal of Climate, 19(15), 3445–3482. https://doi.org/10.1175/JCLI3819.1

https://people.atmos.ucla.edu/alexhall/publications/Hall/Bony_et_al_2005.pdf