The Physics of the Climate Response to Doubling CO2
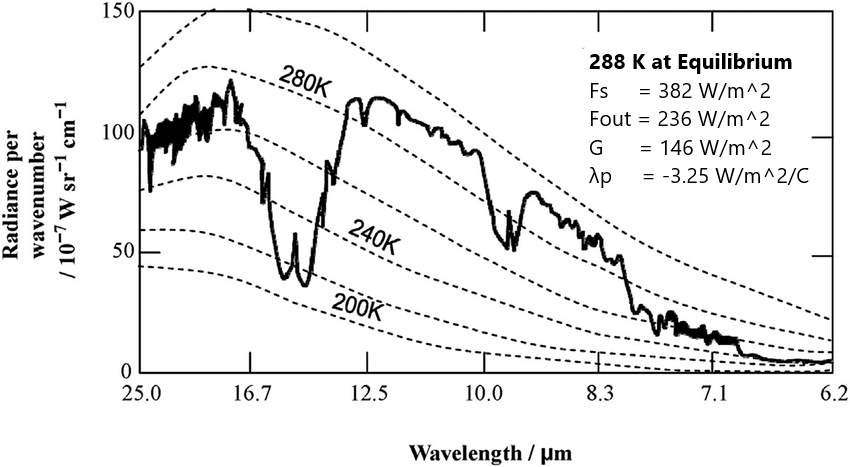
Update (6/6/2025): I edited the text for clarity (especially in the first couple paragraphs), changed g to g̃ to distinguish the normalized GHE from the acceleration due to gravity, and added more references with excerpts at the bottom of the post. The Earth's effective temperature - the mean surface temperature of Earth if the atmosphere contained no GHGs but with current albedo can be calculated since we know that ASR (hereafter Fin) = (1-α)*S/4 and OLR (hereafter Fout) is governed by εσ*T^4. At equilibrium, ASR = OLR (Fin = Fout). With no greenhouse effect (GHE), the Earth's emission temperature (Te) would be at the surface, meaning that Te = Ts, so we can solve for Te with (1-α)*S/4 = εσ*Te^4 If we solve for Te with a surface emissivity ( ε) o f 0.98 and albedo ( α) of 0.306, we end up with Te = 255.3 K. So, if the earth had no atmosphere with albedo roughly the same as today, the average surface temperature of the earth would be about -18°C. ...